Rotary Position Embedding – An Interactive Guide

Rotary Position Embedding (RoPE)

An interactive guide to the math and intuition behind RoPE.

1. The 2D Case: Rotation as Complex Multiplication

For a 2D vector $x_m$ (representing an input token's embedding at position $m$), RoPE applies a linear transformation $W_q$ (e.g., to create a query vector) and then rotates it based on its position $m$. This elegant rotation can be represented using complex numbers. If $W_q x_m$ is viewed as a complex number, its rotation by an angle $m\theta$ is simply:

$ f_q(x_m, m) = (W_q x_m) \cdot e^{im\theta} $

Here, $e^{im\theta} = \cos(m\theta) + i\sin(m\theta)$ is Euler's formula. When expanded, this complex multiplication is equivalent to a standard 2D rotation matrix applied to the vector $(W_q x_m)$:

$ f_q(x_m, m) = \begin{pmatrix} \cos(m\theta) & - \sin(m\theta) \\ \sin(m\theta) & \cos(m\theta) \end{pmatrix} (W_q x_m) $

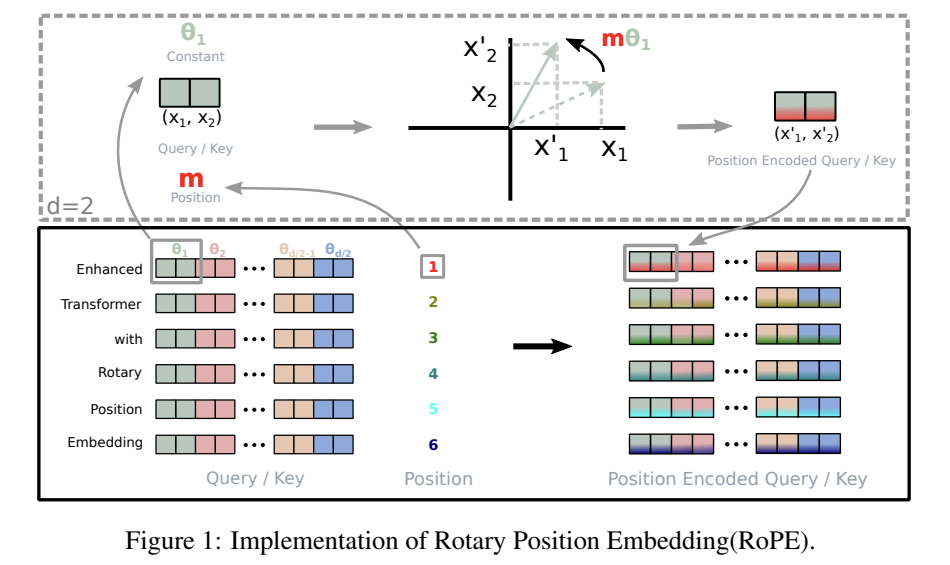
This means each 2D vector is rotated by an angle directly proportional to its position $m$, scaled by a base frequency $\theta$.

2. The General d-Dimensional Form: Block-Diagonal Rotations

RoPE extends this concept to a $d$-dimensional vector by pairing up features. For example, dimensions $(0, 1)$ form the first pair, $(2, 3)$ the second, and so on, up to $(d-2, d-1)$. Each of these $\frac{d}{2}$ pairs is rotated independently. Crucially, each pair uses a different rotation frequency, $\theta_i$, forming a block-diagonal rotation matrix $R^d_{\Theta,m}$:

$ f_q(x_m, m) = R^d_{\Theta,m} W_q x_m $

The rotation frequencies $\theta_i$ for each pair $i \in [0, \frac{d}{2}-1]$ are defined as:

$ \theta_i = \text{base}^{-2i/d} $

Here, `base` is a hyperparameter (commonly $10000$). This formula ensures a spectrum of frequencies: pairs with smaller $i$ (earlier dimensions) have higher frequencies (rotate faster), while pairs with larger $i$ (later dimensions) have lower frequencies (rotate slower). This allows the model to capture both fine-grained and coarse-grained positional information.

3. Application to Self-Attention: Relative Position Encoding

The true power of RoPE shines in the self-attention mechanism. The attention score between a query vector $q_m$ (derived from $x_m$ at position $m$) and a key vector $k_n$ (derived from $x_n$ at position $n$) is their dot product. RoPE's design ensures that this dot product naturally incorporates relative positional information.

$ \begin{aligned} q_m^T k_n &= (R^d_{\Theta,m} W_q x_m)^T (R^d_{\Theta,n} W_k x_n) \\ &= (W_q x_m)^T (R^d_{\Theta,m})^T R^d_{\Theta,n} (W_k x_n) \\ &= (W_q x_m)^T R^d_{\Theta, n-m} (W_k x_n) \end{aligned} $

The key step is $(R^d_{\Theta,m})^T R^d_{\Theta,n} = R^d_{\Theta, n-m}$. This identity, which holds for rotation matrices, means that the combined effect of rotating $q_m$ by $m$ and $k_n$ by $n$ is equivalent to rotating $k_n$ by the relative position $(n-m)$ with respect to $q_m$. This final equation shows that the attention score is no longer a function of the absolute positions $m$ and $n$, but rather a function of the input vectors $x_m, x_n$ and their **relative displacement**, $n-m$. This is how RoPE elegantly injects relative position information directly into the self-attention calculation, which is critical for sequence understanding in models like LLMs.